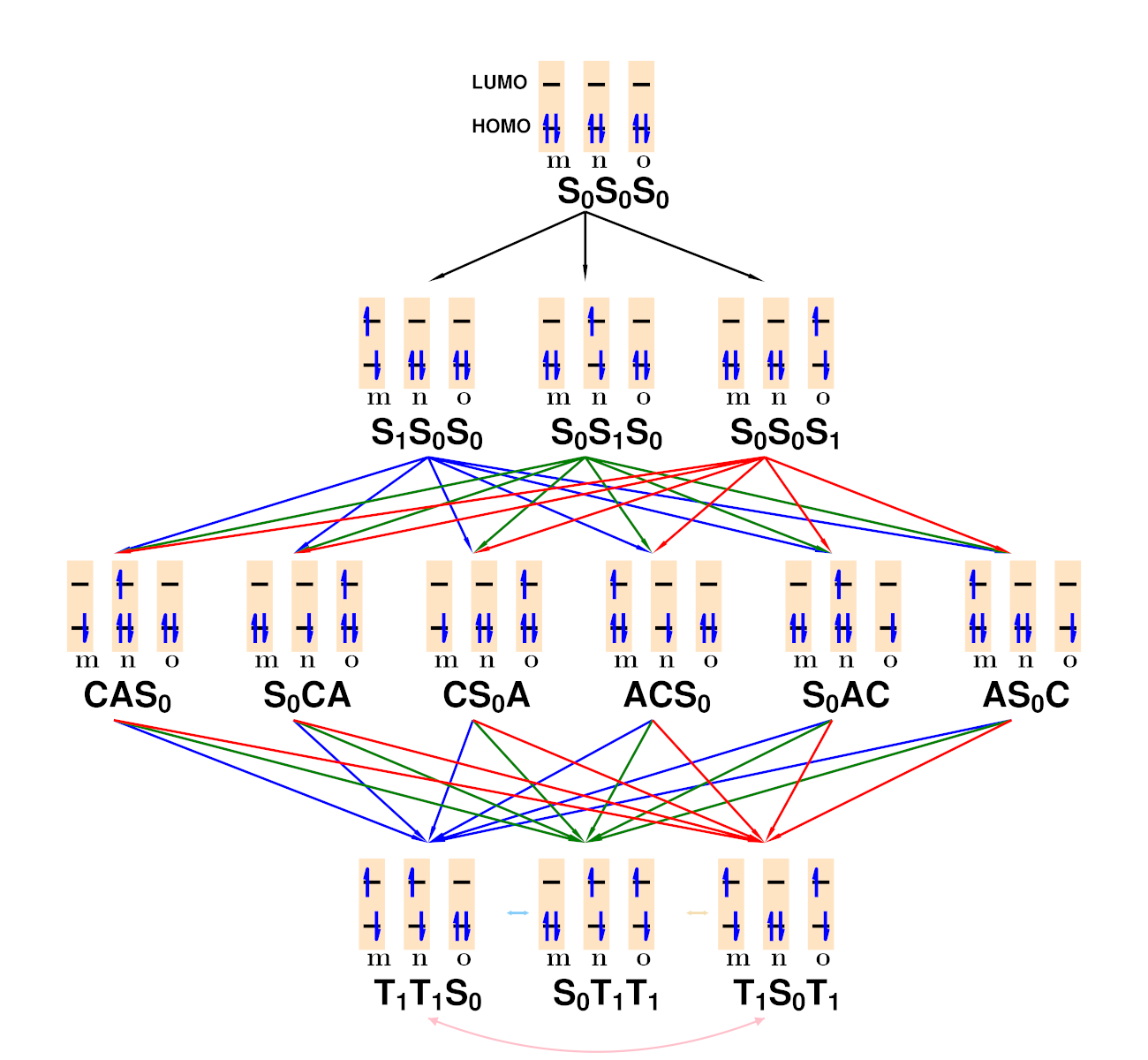
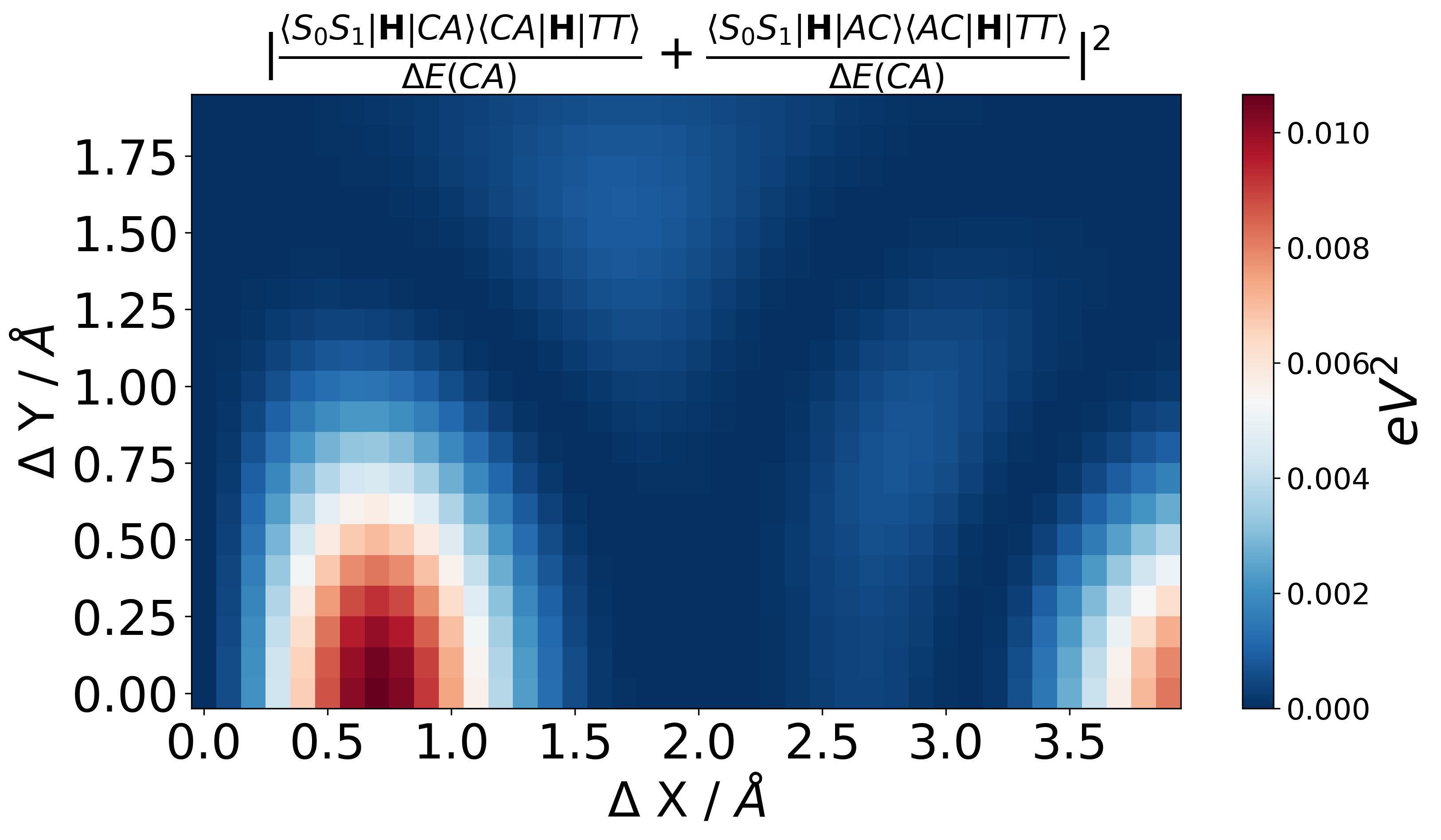
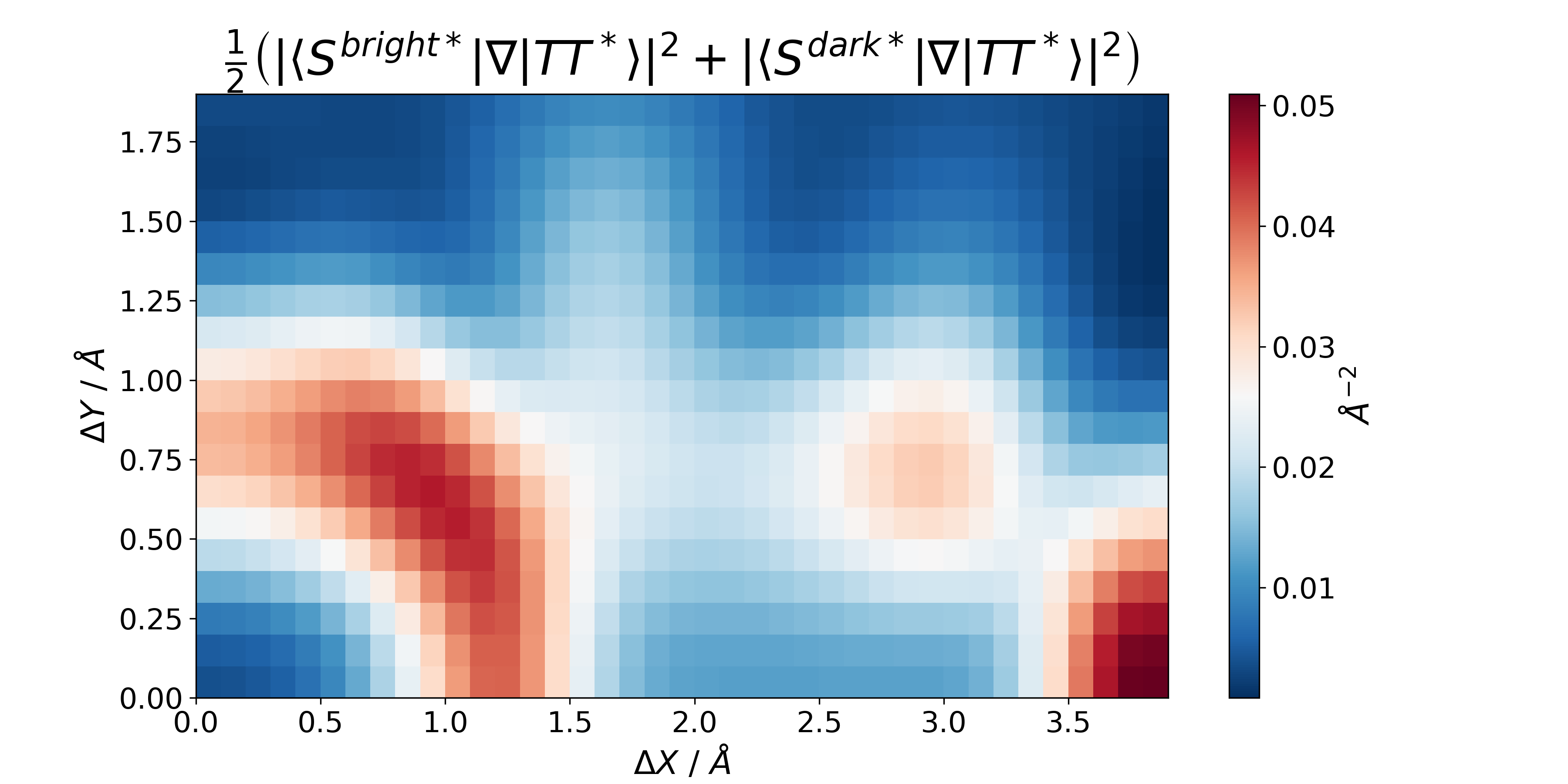
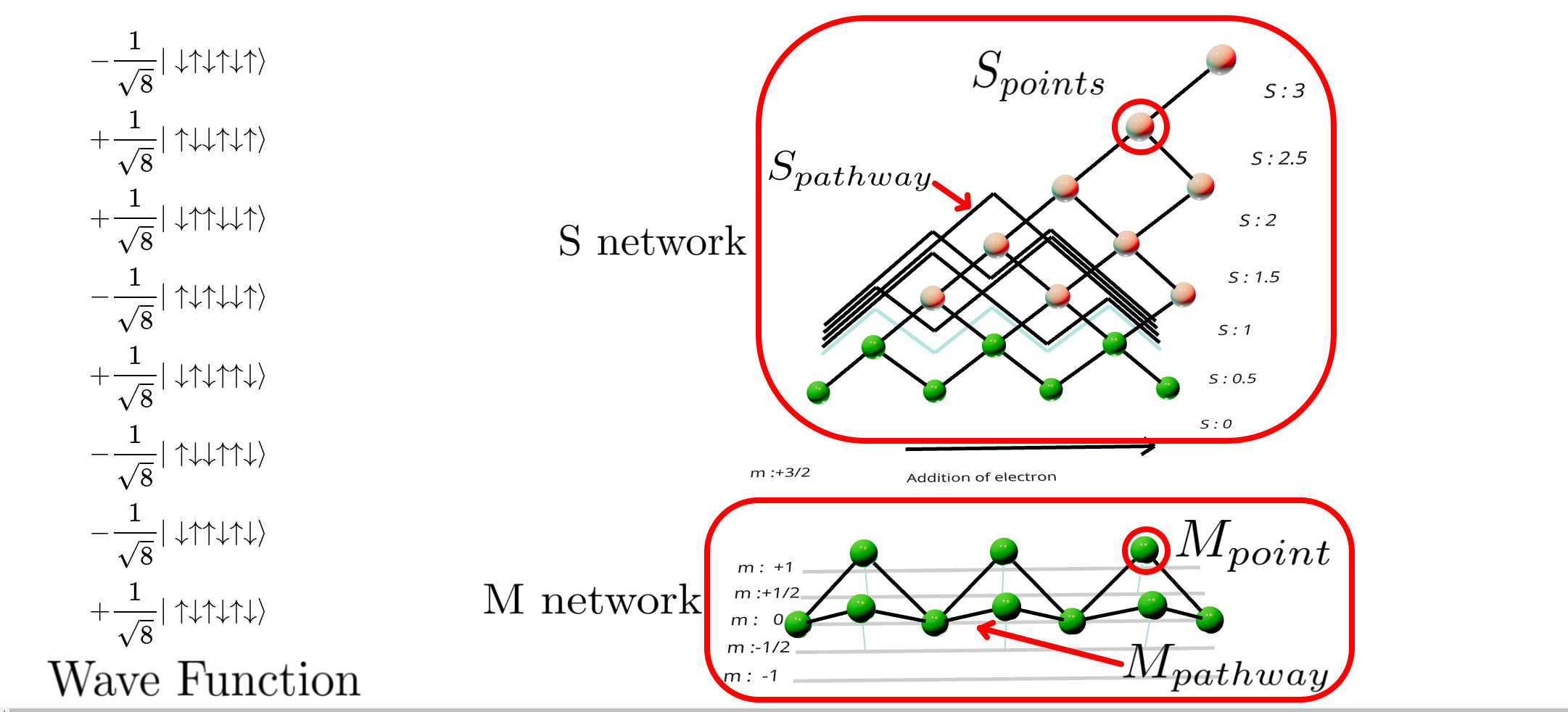
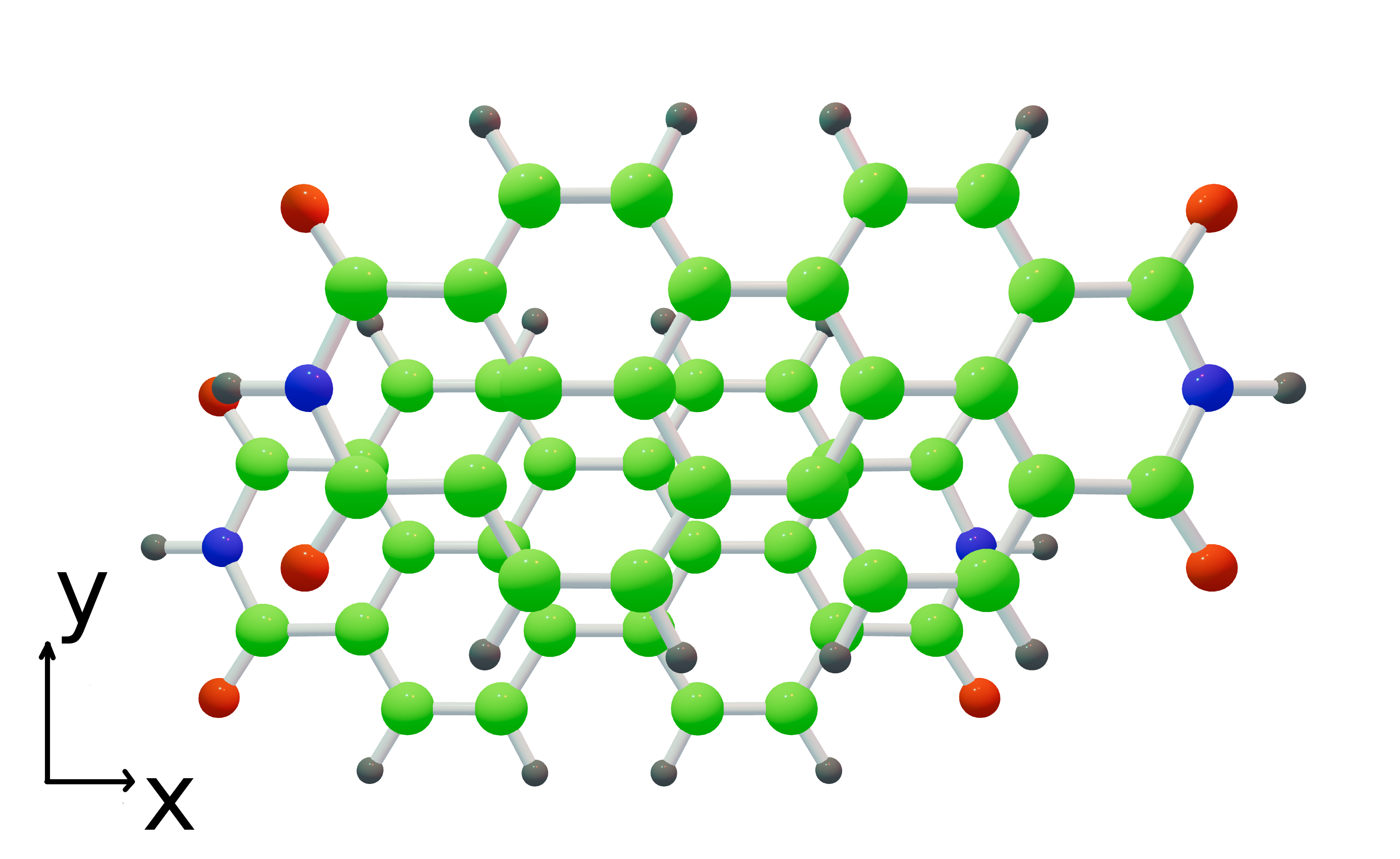
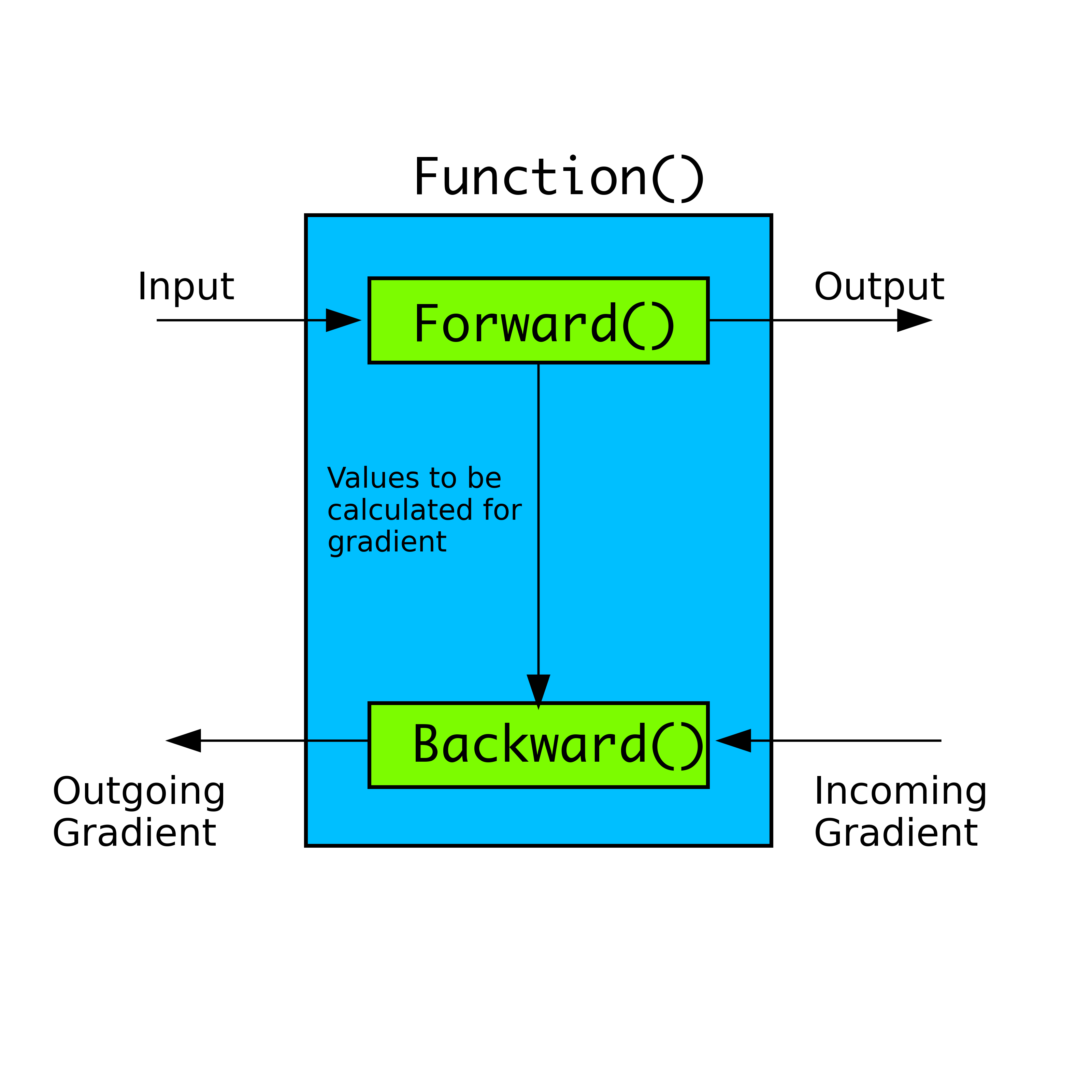
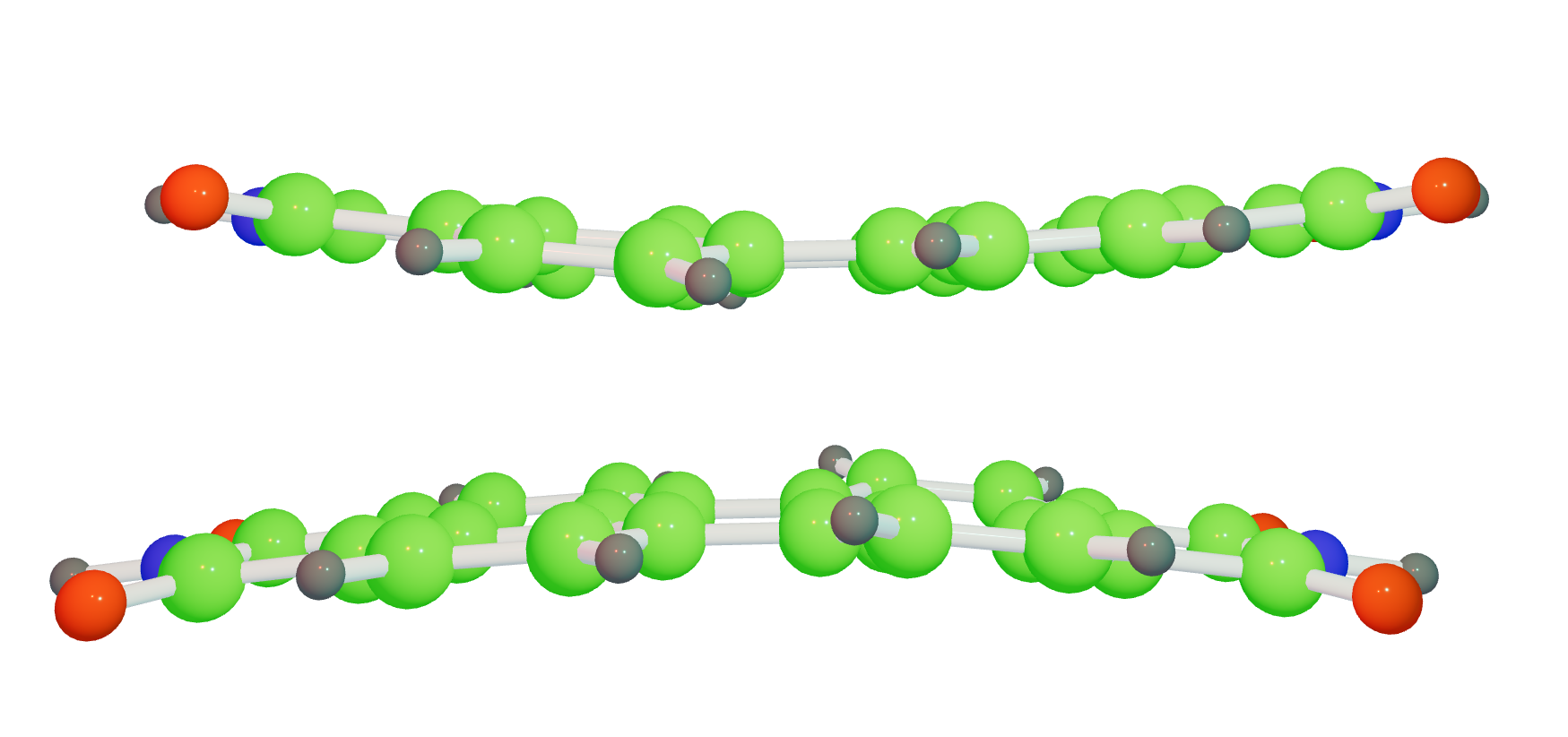
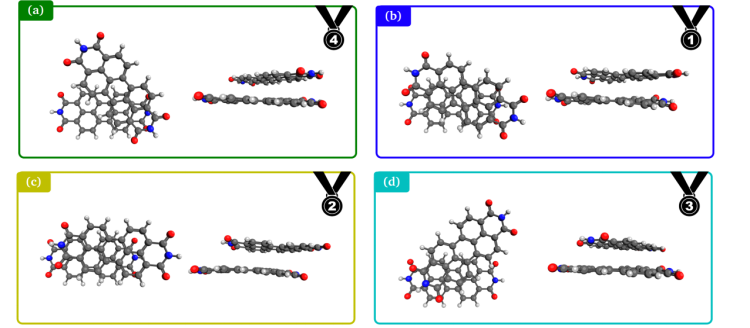
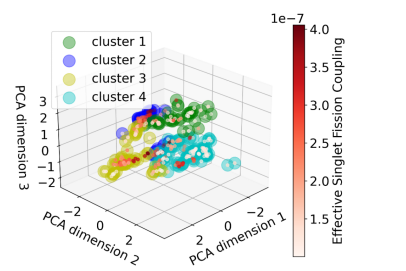
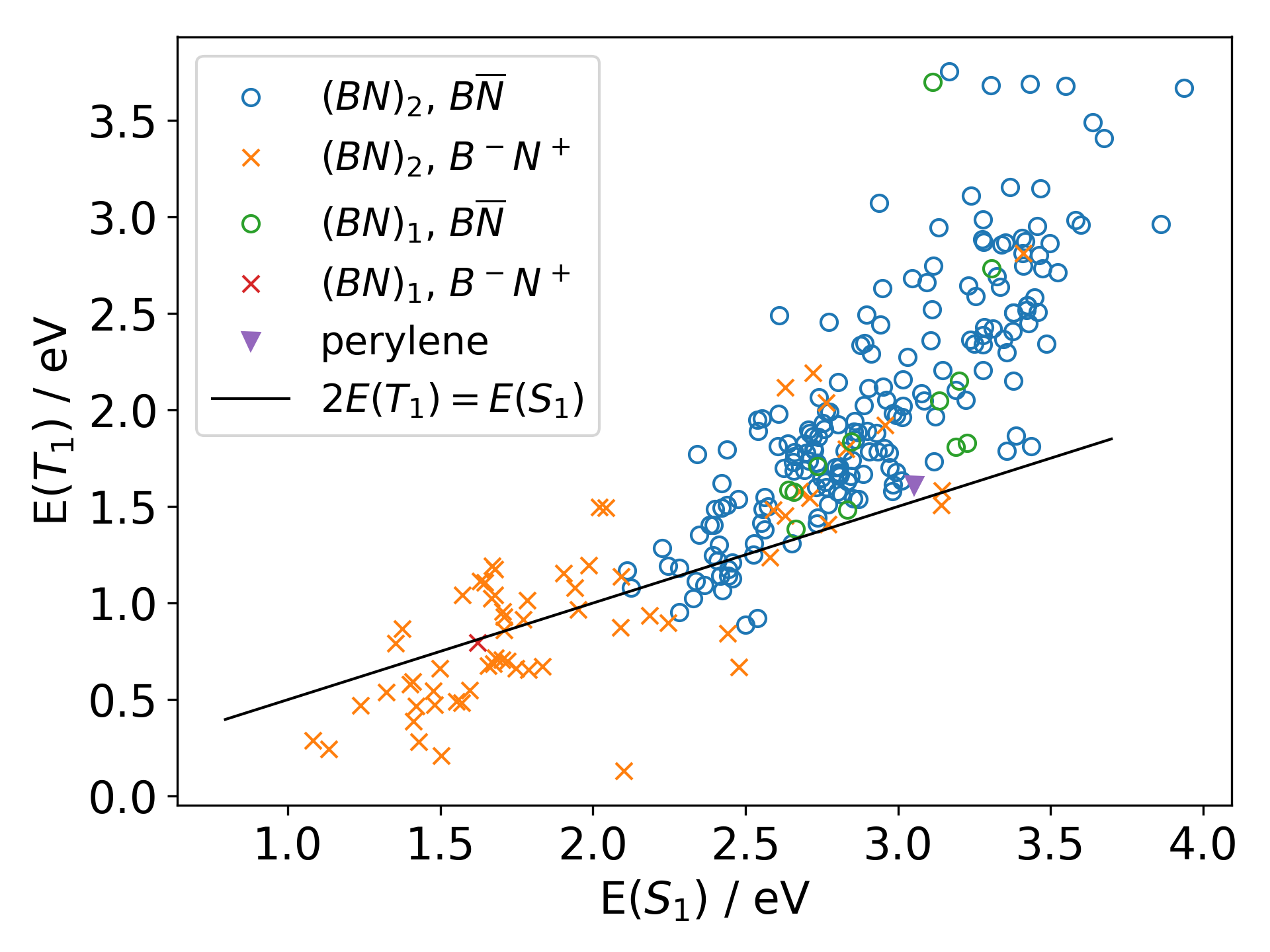
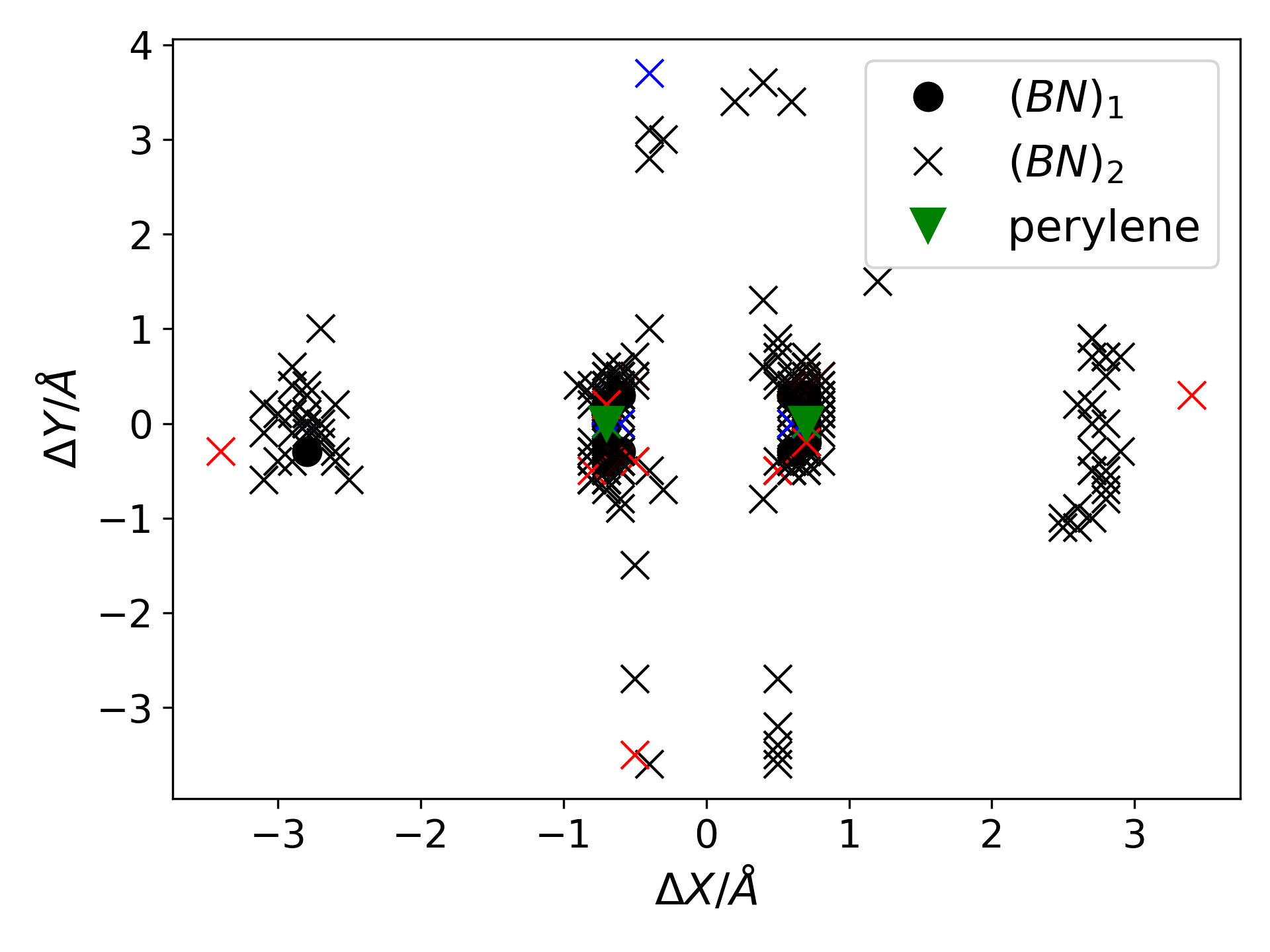
Wave Function Representation
The wave function with spin-only information is expressed as follows:
\( \vert \Psi^{S_{pathway}}_{(^{i}s)} \rangle =
\sum^{M_{pathways}}_{k} CG_{k} \vert s_{1},m_{1} \rangle \otimes \dots \vert
s_{n},m_{n} \rangle \)
Using creation operators, the wave function can be represented as:
\( \vert \Psi^{S_{pathway}}_{(^{i}s)} \rangle = \sum^{M_{pathways}}_{k}
\sum_{k} CG_{k} C^{\dagger}_{\vert s,m\rangle_{j}} \dots \vert - \rangle \)
The Creation and annihilation operator is defined as:
$$
a^{\dagger} = \begin{pmatrix}
0 & 0 \\
1 & 0
\end{pmatrix}
,
a = \begin{pmatrix}
0 & 1 \\
0 & 0
\end{pmatrix}
$$
Creation operator for an electron in spatial orbtal \( \psi
\)
\(\textbf{a}^{\dagger}_{\sigma \psi} = (\mathbf{s} \otimes ....\otimes
\mathbf{s}
\otimes
a^{\dagger}_{\sigma } \otimes \unicode{x1D7D9}^{2} \otimes .... \otimes
\unicode{x1D7D9}^{2})\psi.
\)
\begin{equation}
\begin{split}
\left\langle\Psi_{m}\right|\hat{H}\left|\Psi_{n}\right\rangle = \sum_{i,j =
1}^{d}\sum_{s_{i},s_{j} =
\uparrow,\downarrow}T_{ij}\left\langle\Psi_{m}\right|\textbf{a}_{i,s_{i}}^{\dagger}\textbf{a}_{j,s_{j}}\left|\Psi_{n}\right\rangle
\\ + \frac{1}{2}\sum_{i,j,k,l = 1}^{d}\sum_{s_{i},s_{j},s_{k},s_{l} =
\uparrow,\downarrow}V_{ijkl}\left\langle\Psi_{m}\right|\textbf{a}_{i,s_{i}}^{\dagger}
\textbf{a}_{j,s_{j}}^{\dagger}\textbf{a}_{k,s_{k}}
\textbf{a}_{l,s_{l}}\left|\Psi_{n}\right\rangle,
\label{eq:coup}
\end{split}
\end{equation}